Example 1
Image of formula from Wikipedia
# Split
# No Scale
dataset = [[1, 1], [2, 3], [3, 2], [4, 3], [5, 5]]
x_mean = sum([row[0] for row in dataset])/float(len(dataset))
y_mean = sum([row[1] for row in dataset])/float(len(dataset))
covar = 0
for i in range(len(dataset)):
x = dataset[i][0]
y = dataset[i][1]
covar_iteration = ((x - x_mean) * (y -y_mean)) / (len(dataset) - 1)
covar += covar_iteration
using list comprehension: sum([(row[0] - x_mean) * (row[1] - y_mean) for row in dataset]) / (len(dataset) - 1)
var = 0
for i in range(len(dataset)):
x = dataset[i][0]
var_iteration = (x - x_mean)**2 / (len(dataset) - 1)
var += var_iteration
using list comprehension: sum([(row[0]-x_mean)**2 for row in dataset]) / (len(dataset) - 1)
Bhat = covar / var
Ahat = y_mean - (Bhat * x_mean)
# See stats for sample correlation coefficient, uncorrected sample standard deviations, sample variance, and sample covarianceExample 2 Using Dot Product
Consider yhat = a + bx
Image of formula from StatsHowTo
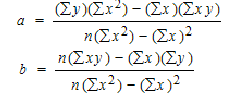
Code credit: https://www.udemy.com/data-science-linear-regression-in-python
x_values = [row[0] for row in dataset]
y_values = [row[1] for row in dataset]
X = np.array(x_values)
y = np.array(y_values)
# X = np.asarray([43, 21, 25, 42, 57, 59])
# y = np.asarray([99, 65, 79, 75, 87, 81])
denominator = y.size * sum(map(lambda x:x*x,X)) - X.sum()**2
# sum(map(lambda x:x*x,X)) same as X.dot(X)
a = ((y.sum() * X.dot(X)) - (X.sum() * sum(X * y))) / denominator
b = ((y.size * sum(X * y)) - (X.sum() * y.sum())) / denominator
print ('y = {:0.4f} + {:0.4f}x'.format(a, b))
# or
d = X.dot(X) - X.mean() * X.sum()
a1 = ( y.mean() * X.dot(X) - X.mean() * X.dot(y) ) / d
b1 = ( X.dot(y) - y.mean() * X.sum() ) / d
print ('y = {:0.4f} + {:0.4f}x'.format(a1, b1))
Example 3 Using Linear Algebra
Code credit: KDNuggets
x_stack = np.vstack(x_array)
x_stack = np.append(arr = np.ones((5, 1)).astype(int), values = x_stack, axis = 1)
print('w = ', np.linalg.inv(x_stack.T.dot(x_stack)).dot(x_stack.T).dot(Y))
or
print('w = ', np.linalg.inv(X.T.dot(X)).dot(X.T).dot(Y))Example 4 using Linear Regression Model
from sklearn.linear_model import LinearRegression
x = [1, 2, 3, 4, 5]
y = [1, 3, 2, 3, 5]
x_r = np.array(x).reshape(-1, 1)
y_r = np.array(y)
model = LinearRegression()
model.fit(x_r, y_r)
print(f'{model.coef_}x + {model.intercept_}')
print(f'Score: {model.score(x_r, y_r)}')
for i, n in enumerate(x):
print(model.predict(np.array([[n]])), y[i])